数据结构笔记 - 排序算法 堆排序算法

|

堆排序：

其基本思想是将待排序的数组构造成一个大顶堆，从而获得数组最大的元素，即当前的根节点。将其移走之后，再把剩余的n-1个数组元素重新构造成一个大顶堆。反复执行，最后得到一个有序序列。

堆排序属于选择排序。

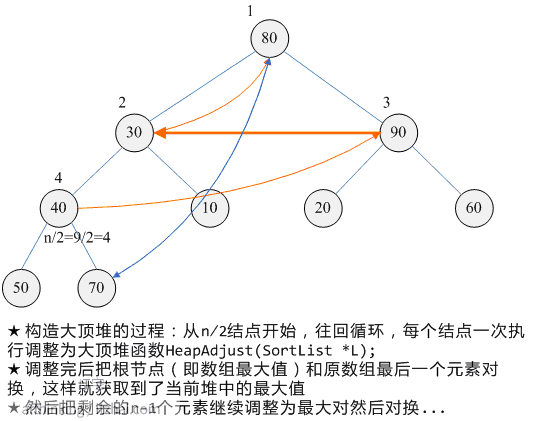
堆排序的过程：

  • ① 循环处理元素构造大顶堆
  • ② 获取堆顶元素并和最后一个叶节点交换位置
  • ③ 重新构建大顶堆，元素个数减一（除去最后一个叶节点，即选出的最大值）。
  • ④ 循环第2、3个步骤。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <stdio.h>

#define MAXSIZE 100  /* 待排序数组的大小 */

typedef struct
{
	int r[MAXSIZE+1];	/* 待排序数组r，r[0]为哨兵或临时变量 */
	int length;			/* 待排序数组的长度，为了方便理解，不包含r[0]元素 */
}SortList;

/* 堆排序算法 */
void HeapSort(SortList *L)
{
	int i;
	/* 把待排序数组L构造成大顶堆 */
	for(i=L->length/2;i>0;i--)
		 HeapAdjust(L,i,L->length);

	for(i=L->length;i>1;i--)
	{
		/* 将当前大顶堆的根节点即数组最大值和未排序钱的数组最后一个元素交换位置 */
		int temp=L->r[1];
		L->r[1]=L->r[i];
		L->r[i]=temp;
		/* 把待排序数组L(1 to i-1)中剩余的元素继续构造成大顶堆 */
		HeapAdjust(L,1,i-1);
	}
}

/* 已知r[s...m]中除了r[s]元素之外均满足堆的定义，本函数通过调整r[s]元素，使待排序数组L构造成大顶堆 */
void HeapAdjust(SortList *L,int s,int m)
{
	int temp,j;
	temp=L->r[s];
	/* 沿着元素比较大的结点往下找 */
	for(j=2*s;j<=m;j*=2)
	{
		/* 比较左子树和右子数的大小，获取较大子数的下标j */
		if(j<m && L->r[j]<L->r[j+1])
			++j;
		/* r[s]已经是最大的，无需改变位置 */
		if(temp>=L->r[j])
			break;
		/* 把较大的子节点赋值给r[s] ，此时r[s]与r[j]相等 */
		L->r[s]=L->r[j];
		/* 从被替换的子节点j开始继续下一个循环，查找j的子节点 */
		s=j;
	}
	/* 此时的r[s]为循环到最后一个处理的父节点 */
	L->r[s]=temp; /* 此时的r[s]为最后一个被交换的子节点，而不是开始的，把temp值赋予该结点，实现和需要处理元素的交换 */
}

堆排序算法复杂度分析：

在初始化构建大顶堆时，每个非终端结点最多比较两次，所有，这个构建的过程时间复杂度为O(n)。

排序过程中，第i次取堆顶记录重建大顶堆的时间复杂度为O(logi)，并且需要取n-1次堆顶记录，所有重建堆的时间复杂度为O(nlogn)。总体上来说，堆排序的时间复杂度为：O(nlogn)。

因为初始化构建堆所需比较次数较多，所以堆排序不适合待排序元素较少的情况。