3、树状数组 Fenwick Tree

3.1、为什么需要Fenwick Tree

假设我们有一个数组A，需要计算数组中[i, j) 区间的数据之和，为了方便获取，我们提前把算好的前面n个元素之和存到另一个数组B的n+1中，如下：

这样我们就很方便的计算区间和了，如：

[2, 5) = B[5] - B[2] = 18 - 6 = 12

但是假设我们想修改A中第i个元素的值，那么B中第i+1之后的元素值都得更新：

也就是说更新的复杂度为O(n)，有没有更好的办法加快更新速度呢？这个时候我们的Fenwick Tree就要出场了，Fenwick Tree也叫Binary Indexed Tree(二元索引树)。

3.2、什么是Fenwick Tree

Fenwick Tree是一种支持给静态数组范围求和，以及在静态数组中更新元素的值后也能够进行进行范围求和的数据结构。

最低有效位(LSB least significant bit)：静态数组的小标可以转换为二进制，如8：01000，最低有效位指的是从右往左数，不为0的位，这里为 1000，计算数组小标最低有效为的函数我们一般命名为lowbit，实现参考后续代码。

数组下标的最低有效位的值n，表示该下标存储了从该下标往前数n位元素的数值之和。如下图：

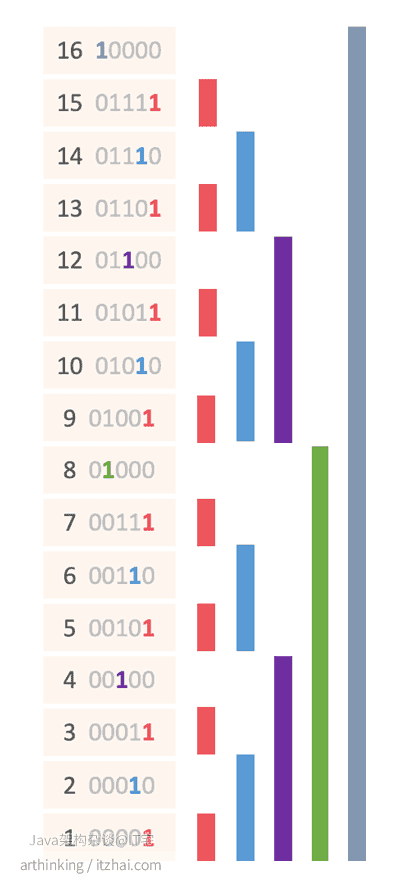
我们可以发现：

1：只保存当前下标元素的值，对应上面红色区块；
10：保存下标往前数总共2个元素的值，对应上面蓝色区块；
100：保存下标往前数总共4个元素的值，对应上面紫色区块；
1000：保存下标往前数总共8个元素的值，对应上面绿色区块；
10000：保存下标往前数总共16个元素的值，对应上面浅蓝色区块；

3.2.1、范围求和

有了上面的数据结构，我们就可以进行范围求和了。

假设我们要求和[1, 7]，我们只要把以下红色区块值相加就可以了，也就是 sum = B[7] + B[6] + B[4]

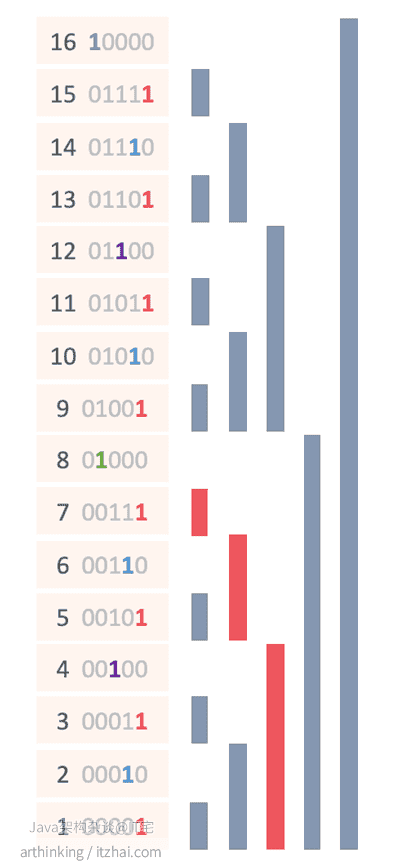
如果我们要求和[10, 14]，那么我们可以这样处理：sum = sum[1, 14] - sum[1, 9] = (B[14] + B[12] + B[8]) - (B[9] + B[8])。

也就是说，针对范围查询，我们会根据LSB一直回溯上一个元素，然后把回溯到的元素都加起来。

最差的情况下，求和的复杂度为：O(log2(n))

以下是实现范围求和的代码：

/**
 * 求和 [1, i]
 */
public int prefixSum(int i) {
  sum = 0;
  while(i != 0) {
    sum = sum + tree[i]
    i = i = lowbit(i);
  }
  return sum;
}

/**
 * 求和 [i, j]
 */
public int rangeQuery(int i, int j) {
  return prefixSum(j) - prefixSum(i - 1);
}

3.2.2、单点更新

更新数组中的某一个元素的过程中，与范围查询相反，我们不断的根据LSB计算到下一个元素位置，同时给该元素更新数组。如下，更新A[9]，会级联查找到以下红色的位置的元素：

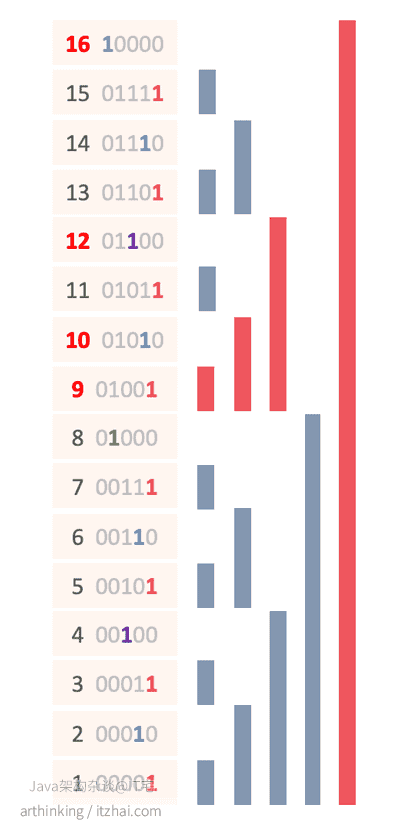
以下是实现代码，给第i个元素+x：

public void add(int i, int x) {
  while (i < N) {
    tree[i] = tree[i] + x;
    i = i + lowbit(i)
  }
}

3.2.3、构造Fenwick Tree

假设A为静态数组，B数组存放Fenwick Tree，我们首先把A数组clone到B数组，然后遍历A数组，每个元素A[i]依次加到下一个负责累加的B节点B[i + LSB]中(称为父节点)，直到到达B数组的上界，代码如下：

public FenwickTree(int[] values) {
    N = values.length;
		values[0] = 0L;

		// 为了避免直接操纵原数组，破坏了其所有原始内容，我们复制一个values数组
		tree = values.clone();

		for (int i = 1; i < N; i++) {
			// 获取当前节点的父节点
			int parent = i + lowbit(i);
			if (parent < N) {
				// 父节点累加当前节点的值
				tree[parent] += tree[i];
			}
		}
}

思考：如果我们想要快速更新数组的区间范围，如何实现比较好呢？参考：

3.3、时间复杂度

操作	时间复杂度
construction	O(n)
point update	O(log(n))
range sum	O(log(n))
range update	O(log(n))
adding index	/
removing index	/

3.4、编程实践

单点更新，区间查找：FenwickTreeRangeQueuePointUpdate
区间更新，单点查找：FenwickTreeRangeUpdatePointQuery
练习：
- Range Sum Query - Mutable

数据结构与算法

Fenwick Tree数据结构