二叉树的前序遍历、中序遍历和后序遍历及其算法

二叉树的基本的遍历规则有三种：前序遍历，中序遍历和后序遍历。对于每一种遍历，树中每个结点都要经过3次。前序遍历在第一次遇到结点时立即访问，中序遍历第二次遇到结点时访问，后序遍历则到第三次遇到结点时才访问。

以一棵二叉树说明其三种遍历顺序：

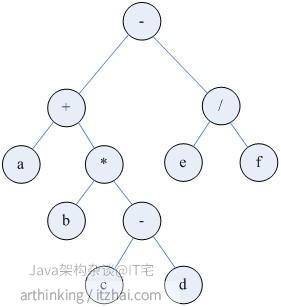
前序遍历：

- + a * b – c d / e f

中序遍历：a + b * c – d – e / f

后序遍历：a b c d – * + e f / -

前序遍历算法：

template<class T>
void BinaryTree<T>::PreOrder(BinTreeNode<T> *subTree,
		       void (*visit)(BinTreeNode<T> *P)) {
	//递归函数：此算法按照前序遍历以subTree为根的二叉树。
	if(subTree!=NULL){		//递归结束条件
		visit(subTree);		//访问根节点
		PreOrder(subTree->leftChild,visit);	//前序遍历根的左子树
		PreOrder(subTree->rightChild,visit);	//前序遍历根的右子树
	}
};

中序遍历算法：

template<class T>
void BinaryTree<T>::InOrder(BinTreeNode<T> *subTree,
		       void(*visit)(BinTreeNode<T> *p)){
	//递归函数：此算法按照中序次序遍历以subTree为根的子数
	if(subTree!=NULL) {		//如果subTree为NULL，则结束递归
		InOrder(subTree->leftChild,visit);	//中序遍历根的左子树
		visit(subTree);	//访问根节点
		InOrder(subTree->rightChild,visit);	//中序遍历根的右子数
	}
};

后序遍历算法：

template<class T>
void BinaryTree<T>::PostOrder(BinTreeNode<T> *subTree,
			void (*visit)(BinTreeNode<T> *P)) {
	//递归函数，此算法按照后序遍历以subTree为根的二叉树
	if(subTree!=NULL) {		//递归结束条件
		PostOrder(subTree->leftChild,visit);	//后序遍历根的左子树
		PostOrder(subTree->rightChild,visit);	//后序遍历根的右子树
		visit(subTree);		//访问根节点
	}
};