9、二叉树与二叉搜索树BST

**二叉树(Binary Tree)**是每个节点最多具有两个子节点的树；

**二叉搜索树(Binary Search Tree)**是满足以下条件二叉树：左子树的元素较小，右子树的元素较大。

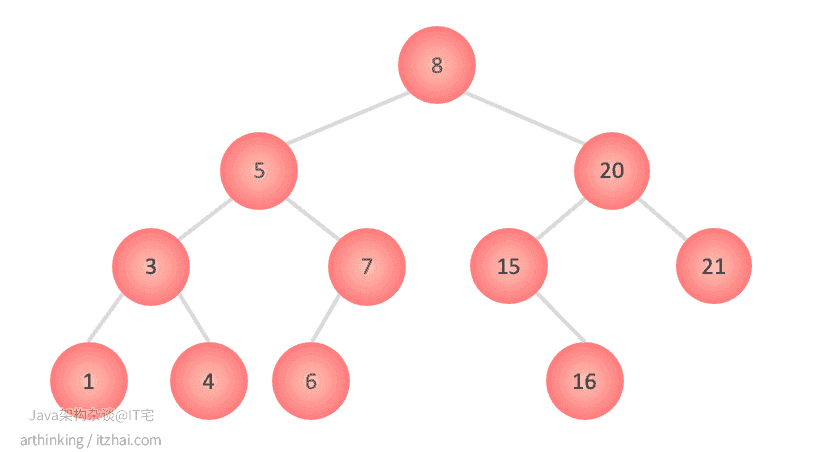
9.1、使用场景

某些map和set的ADT的实现；
红黑树；
AVL树；
伸展树(Splay Tree 分裂树)；
用于二叉堆的实现；
语法树；
Treap-概率DS(使用随机BST)

9.2、实现思路

9.2.1、插入元素

二叉搜索树（BST）元素必须具有可比性，以便我们可以在树中对其进行排序；
插入元素时，我们将其值与当前节点中存储的值进行比较：
- 小于节点值：向下递归左子树；
- 大于节点值：向下递归右子树；
- 等于节点值：处理重复值；
- 不存在节点：创建新节点。

极端场景：

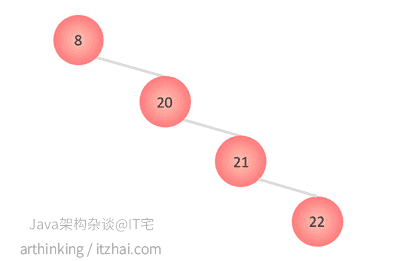
这种情况就变为了线性结构，比较糟糕，这就是平衡二叉搜索树出现的原因。

9.2.2、移除元素

移除元素可以分为两步：

找到我们想要移除的元素；
如果存在后续节点，那么我们用后续节点替换掉要删除的节点；

移除会有以下三种情况：

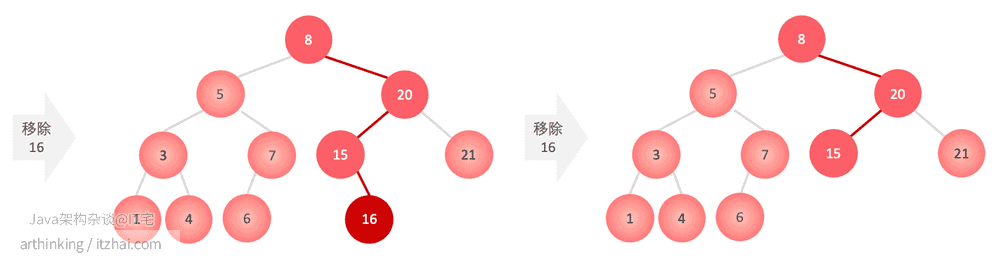
9.2.2.1、移除的元素是一个叶子节点

找到对应待移除的节点，直接删除掉即可：

remove(16)：

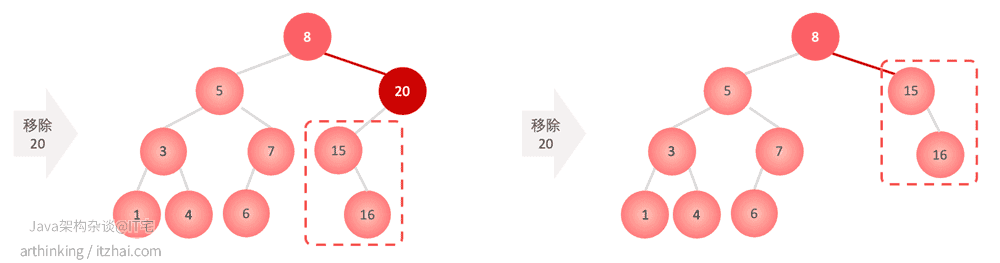
9.2.2.2、移除的元素下面有左子树或者右子树

如果移除的元素下面带有左子树或者右子树，那么：找到对应待移除的节点，用子树的根节点作为移除元素的后继者，替换掉需要移除的元素即可：

9.2.2.3、移除的元素下面有左子树和右子树

如果移除的元素下面带有左子树和右子树，那么应该用左子树还是右子树中的节点作为删除元素的后继者呢？

答案是两者都可以！后继者可以是左侧子树中的最大值，也可以是右侧子树中的最小值。

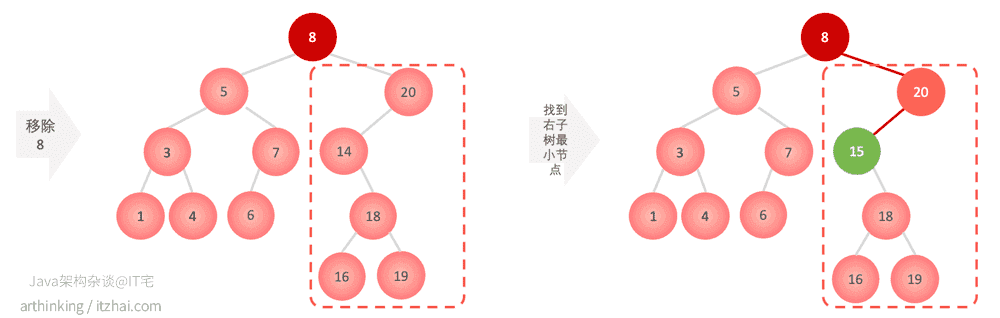
下面我们执行remove(8)，统一选择使用右子树中的最小值。

具体步骤：

查找到需要删除的元素；
在其右子树中寻找到最小值的节点；
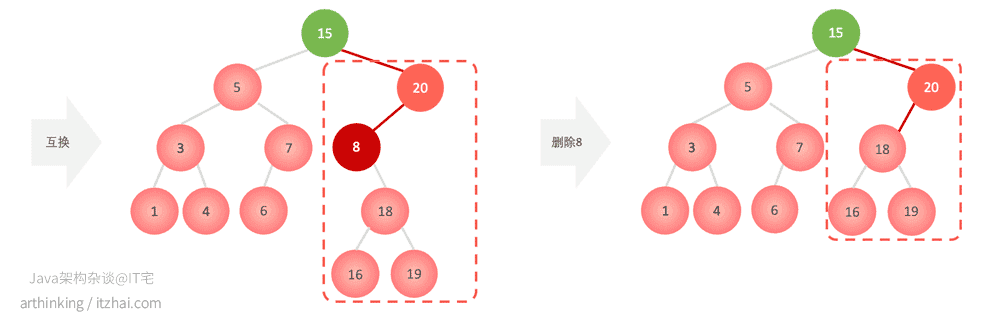
最小值的节点和待删除元素的值互换；
使用9.2.2.2的步骤删除掉原来最小值节点位置的节点；

9.2.3、查找元素

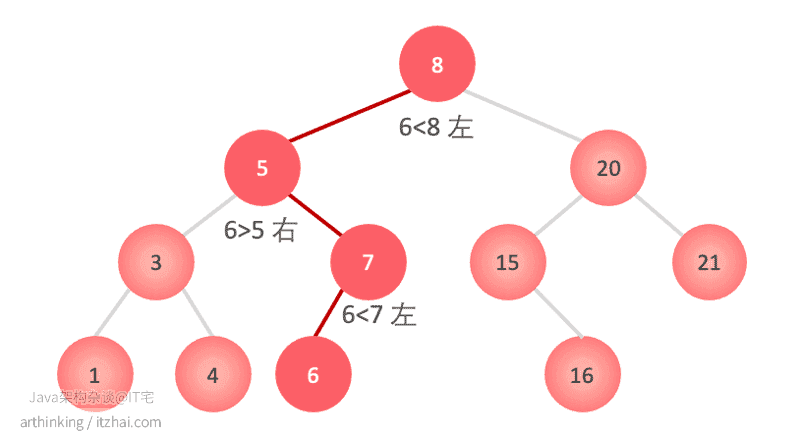
BST搜索元素会出现以下四种情况之一：

我们命中了一个空节点，这时我们知道该值在我们的BST中不存在；
比较器值等于0，说明找到了元素；
比较器值小于0，说明元素在左子树中；
比较器值大于0，说明元素在右子树中。

以下是find(6)操作：

9.3、树的遍历

可以分为深度优先遍历和广度优先遍历。而深度优先遍历又分为：前序遍历、中序遍历、后序遍历、层序遍历。

9.3.1、深度优先遍历

深度优先遍历都是通过递归来实现的，对应的数据结构为栈。

9.3.1.1、前序遍历

在递归方法最开始处理节点信息，代码逻辑：

void preOrder(node) {
  if (node == null) return;
  print(node.value);
  preOrder(node.left);
  preOrder(node.right);
}

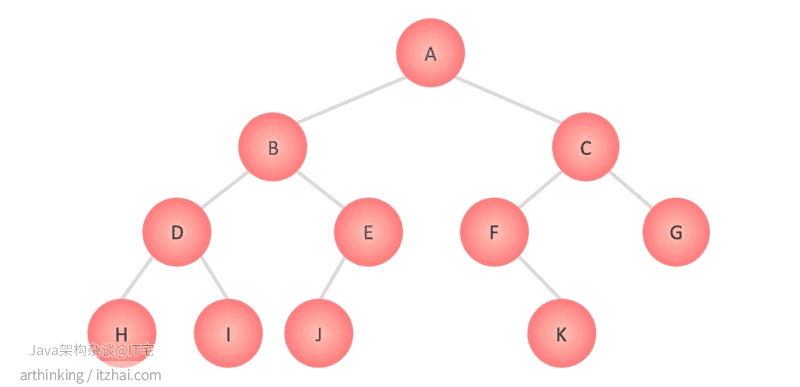
如下二叉树将得出以下遍历结果：A B D H I E J C F K G

9.3.1.2、中序遍历

在递归调用完左子节点，准备右子节点之前处理节点信息，代码逻辑：

void inOrder(node) {
  if (node == null) return;
  inOrder(node.left);
  print(node.value);
  inOrder(node.right);
}

二叉搜索树使用中序遍历，会得到一个排好序的列表。

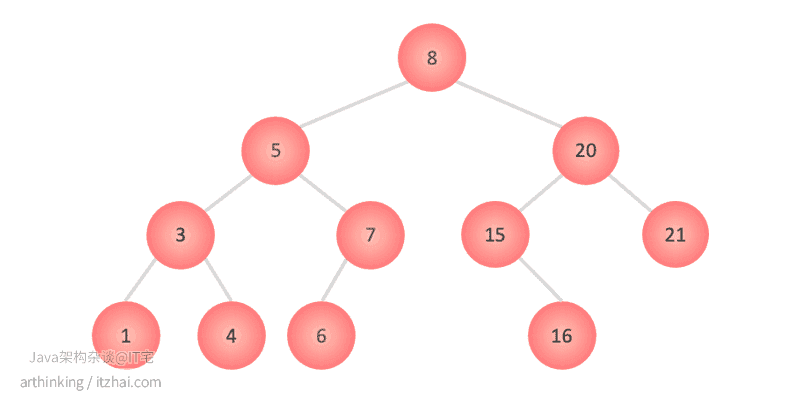
以下二叉搜索树将得出如下遍历结果：1 3 4 5 6 7 8 15 16 20 21

9.3.1.3、后序遍历

在递归完左右子树之后，再处理节点信息，代码逻辑：

void postOrder(node) {
  if (node == null) return;
  postOrder(node.left);
  postOrder(node.right);
  print(node.value);
}

以下二叉树得出如下遍历结果：1 4 3 6 7 5 16 15 21 20 8

9.3.2、广度优先遍历

在广度遍历中，我们希望一层一层的处理节点信息，常用的数据结构为队列。每处理一个节点，同时把左右子节点放入队列，然后从队列中取节点进行处理，处理的同时把左右子节点放入队列，反复如此，直至处理完毕。

9.4、BST时间复杂度

操作	平均	最差
insert	O(log(n))	O(n)
delete	O(log(n))	O(n)
search	O(log(n))	O(n)

9.5、编程实践

BST.java
练习：
- BiNode

数据结构与算法

二叉树数据结构