题目分析

题目要求对链表中的每个k个节点进行翻转，如果链表中的节点数不是k的整数倍，那么保留最后剩余的节点。

注意，题目给的是单向链表。

解题思路

可以使用一种结合了迭代和局部翻转函数的方法来解决该问题。

哨兵节点(dummy)：通过添加一个哑节点（或称为哨兵节点）作为链表的头部，可以简化头节点翻转和链表操作的复杂度，尤其是在处理头节点翻转时避免额外的条件判断；
迭代寻找子列表：通过两个指针pre和end在原始链表上迭代，以k个节点为一组来定位每个子列表的起始和结束位置。pre标记了当前待翻转子列表的前一个节点，而end用于寻找每个子列表的结束节点；
局部翻转和重新连接
更新指针：翻转完成后，pre和end指针更新到当前子列表的末尾节点，即start，为处理下一个子列表做准备；
局部翻转函数(reverse)：一个辅助函数，用于实现链表的局部翻转。该函数通过迭代方法将传入的链表进行翻转，并返回翻转后的头节点。

局部翻转函数指针维护比较复杂，如果想不明白，那就画一个图：

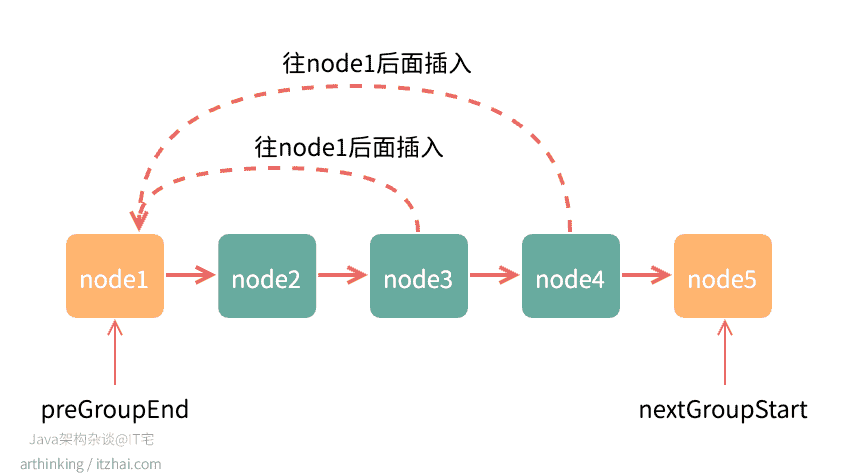
如上图，一次遍历绿色节点，进行翻转数组：

第一个绿色节点node2最终会变为翻转后的最后一个节点；
从node3开始的绿色节点，依次往node1后面插队，最终实现链表翻转；
注意，每处理一个节点，都要维护node2的next指针，执行当前处理节点的下一个节点，以及node1的指针，指向当前处理节点。

Java解法

下面是使用Java语言的解法：

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        if (head == null || k == 1) return head;

        ListNode dummy = new ListNode(0);
        dummy.next = head;
        ListNode preGroupEnd = dummy, current = head;
        
        // 计数，确保有足够的节点进行翻转
        int count = 0;
        while (current != null) {
            count++;
            if (count % k == 0) {
                // 当累积到k个节点，执行翻转，并更新preGroupEnd指针
                preGroupEnd = reverseGroup(preGroupEnd, current.next);
                current = preGroupEnd.next;
            } else {
                // 否则，继续向前移动current指针
                current = current.next;
            }
        }
        
        return dummy.next;
    }

    // 翻转链表从start到end之间的节点，返回翻转后的最后一个节点，作为下一组翻转的前一个节点
    private ListNode reverseGroup(ListNode preGroupEnd, ListNode nextGroupStart) {
        ListNode lastReversed = preGroupEnd.next; // 翻转后的链表的最后一个节点，即图中的node2节点
        ListNode cur = preGroupEnd.next.next; // 当前要处理的节点
        while (cur != nextGroupStart) {
          	// cur 节点往preGroupEnd后面插队
          	// 先处理lastReversed节点，链接到cur的下一个节点
            lastReversed.next = cur.next;
            cur.next = preGroupEnd.next;
            preGroupEnd.next = cur;
          	// 处理下一个节点
            cur = lastReversed.next;
        }
        return lastReversed;
    }
}

时间复杂度

遍历链表：算法首先通过一次遍历来计算链表长度并按照K个节点的组进行翻转。每个节点在遍历过程中被访问一次，以确定翻转的分组。
翻转操作：对于链表中的每个节点，翻转操作在每K个节点的组内进行一次。翻转操作本身需要对每个分组中的节点进行一次遍历，以重新排列指针。

因此，整个链表的每个节点都被访问并处理一次，所以总的时间复杂度为O(N)，其中N是链表中的节点总数。

空间复杂度

辅助空间：算法实现中，主要使用了固定数量的变量（如preGroupEnd，current，和nextGroupStart等）来帮助标识翻转的起始和结束位置，以及进行节点翻转操作。
递归调用栈：由于该算法使用的是迭代方法而非递归，因此不会产生额外的调用栈空间。

综上所述，这个算法的空间复杂度为O(1)，因为它只使用了少量的辅助空间，且与链表长度N无关。

References

25. K 个一组翻转链表 ↩︎

趣味算法题

迭代+局部翻转：K个一组翻转链表